The macroscopic fundamental diagram provides insights on traffic flow at a macroscopic level. Given its elegance, it has become a popular tool to analyse various traffic-related problems. We show that the MFD can also be used to estimate the level of heterogeneity in a network, which allows city planners the possibility to analyse the efficiency of their road network.
The macroscopic fundamental diagram (MFD) relates the average traffic density to the average flow in an urban network. Under relatively homogeneous conditions, a well-defined MFD exists, where the average traffic flow increases with the average traffic density until a maximum is reached. Afterwards, the flow reduces with increasing traffic density. In other words, the MFD offers an elegant way to model traffic flow macroscopically. It has been shown that the MFD is determined mainly by the urban road structure, traffic control (Geroliminis & Daganzo, 2007), and the level of inhomogeneity in the distribution of traffic (Daganzo, Gayah, & Gonzales, 2011; Gayah & Daganzo, 2011; Knoop, van Lint, & Hoogendoorn, 2015). Even though it was shown that the MFD exists in simulations as well as in the real world, there remains much uncertainty in the estimation of the MFD under real-world traffic conditions and urban dynamics.
New Re-sampling Methodology
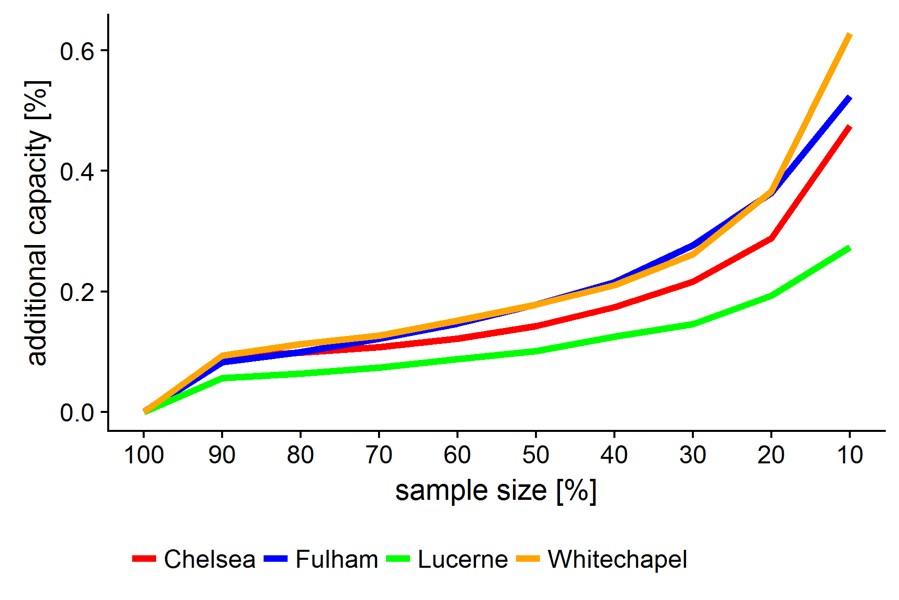
We propose a new re-sampling methodology that allows estimating the level of heterogeneity. Knowing the level of homogeneity allows to evaluate how efficient the road infrastructure is used by vehicles. Generally, the MFD is derived by a length-weighted average of flows and densities across all links in a city. This method, however, might not offer a complete view of traffic conditions. During the morning commute, for example, roads leading into the city are more congested than those leading out. Taking averages of flow and density might provide an estimate on the actual mean performance of the network, but not on the potential performance (i.e. when all links are similarly congested). Therefore, the rationale of our proposed method is therefore to determine the least inhomogeneous sub-samples by first creating many random sub-samples of the network and then estimating an MFD for each. The image shows the capacity gained for various sample sizes for the city of Lucerne and four regions in London. For example, if the entire network behaved like the 10% best links, the additional traffic capacity could increase by 25%. We conclude that the area below such curves is directly related to the heterogeneity of a network and gives city planners the possibility to analyse the efficiency of their road network.
Lukas Ambühl and Allister Loder are PhD students at the Institute for Transport Planning and Systems since 2015 and 2016, respectively. Both are interested in understanding and modeling congestion at the city level. Lukas focuses on the traffic engineering side, whereas Allister focuses on the transport planning perspective. Co-author: Dr. Monica Menendez. They are funded by ETH Research Grants ETH-04 15-1 and ETH-27 16-1. We especially thank Thomas Karrer and Milena Scherer from the city of Lucerne and Ashley Turner and Andy Emmonds from Transport for London (TfL) for their collaboration.
This text is based on the full article: Ambühl, Lukas; Loder, Allister; Menendez, Monica; Axhausen, Kay W. (2018): Introducing a re-sampling methodology for the estimation of empirical macroscopic fundamental diagrams. Transport Research Record. (in print)
Other References
Daganzo, C. F.; Gayah, V. V.; Gonzales, E. J. (2011): Macroscopic relations of urban traffic variables: Bifurcations, multivaluedness and instability. Transportation Research Part B: Methodological, 45(1). S.278–288. https://doi.org/10.1016/j.trb.2010.06.006
Gayah, V. V.; Daganzo, C. F. (2011): Clockwise hysteresis loops in the Macroscopic Fundamental Diagram: An effect of network instability. Transportation Research Part B: Methodological, 45(4). S.643–655. https://doi.org/10.1016/j.trb.2010.11.006
Geroliminis, N.; Daganzo, C. F. (2007): Macroscopic modeling of traffic in cities. In: TRB 86th Annual Meeting (S. 07–0413). Retrieved from http://moodle.epfl.ch/file.php/7471/2011_/Macroscopic_FD.pdf
Knoop, V. L.; van Lint, H.; Hoogendoorn, S. P. (2015): Traffic dynamics: Its impact on the Macroscopic Fundamental Diagram. Physica A: Statistical Mechanics and Its Applications, 438. S.236–250. https://doi.org/http://dx.doi.org/10.1016/j.physa.2015.06.016